Математика и программирование : маленькие заметки.
В примере сжатия по алгоритму Хаффмана (compr.html) автору
для сохранения таблицы (или же просто дерева) потребовалось
около 50 байт. Но я хочу вам рассказать о методе кодирования
деревьев, известного из дискретной математики. При использовании
этого метода для сохранения полной структуры дерева из примера потребуется
всего 2.5 байта + 6 байт для алфавита.
|
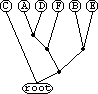
Рисунок 1.
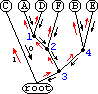
Рисунок 2.
| |
На рисунке слева представлено бинарное дерево из примера.
Для описания метода кодирования надо принять несколько обозначений
и соглашений. Движением вперед будем называть продвижение по дереву от корня к листьям.
На рисунке 2 движение вперед обозначается красными стрелками, черными обозначается движение назад.
По одному ребру дерева можно проходить только два раза - вперед и назад,
после этого ребро должно удаляться из рассмотрения. Для сохранения пути движения
за "1" обозначим движение вперед, за "0" - движение назад. Для кодирования используется обход дерева.
|
Давайте начнем обход дерева. Условимся двигаться слева направо. Таким образом первым
нашим движением будет - из "ROOT" в "C". Здесь мы двигались вперед значит запоминаем "1" в нашей закодированной последовательности.
Теперь мы находимся в "C" и дальше двигаться вперед уже не можем, значит двигаемся назад и запоминаем "0".
Мы находимся снова в "ROOT", но идти снова в "С" мы не можем, так как мы прошли по нему уже два раза, т.е. мы убираем его из рассмотрения.
Таким образом мы можем идти только в узел "3", сохраняем "1". Узел "3" не является вершиной дерева, и кроме того у него есть ребра по которым мы еще не проходили.
Так как мы идем слева на право, то сдедующим движением будет из "3" в "2", запоминаем "1". После того как мы окажемся в "А" движение вперед будет невозможным, и начнется движение назад.
Т.е. из "А" в "1" с сохранением "0". Находясь в узле "1" снова двигаться в "А" мы уже не можем и будем двигаться в "D".
И так далее пока мы не пройдем по всем ребрам по 2 раза.
В результате у нас получится закодированная последовательность:
10111101001001101000
Ее длина 20 бит, что составляет всего 2.5 байта. Таким образом с сжатом файле
полнотью сохраненное дерево будет занимать 2.5+6 байт, т.е. 9 полных байт.
Теперь длина сжатого файла уже будет не 80 байт, а всего 9+30=39 байт, что само
по себе просто замечательно, ведь закодировав просто дерево нам удалось достичь
большего сжатия, чем прежде. Конечно при сжатии файлов в мегабайты, экономия в данном алгоритме
не имеет никакого значения, но при маленьких размерах файла позволяет съэкономить несколько десятков байт.
By Dron (MJK Net)

