Прежде чем разбираться с узлом IndexedFaceSet нам надо разобраться с узлом Coordinate. Определяется он следующим образом:
Coordinate {
exposedField MFVec3f point []
}
Этот узел предельно прост в определении. Его единственный параметр-массив point[] определяет набор точек в трехмерном пространстве. Пример:
Coordinate {
point [
0 0 0 #1 точка
1 0 0 #2
0 1 0 #3
0 0 1 #4
1 1 1 #5
]
}
Данный пример создаст в трехмерном пространстве такой набор точек:
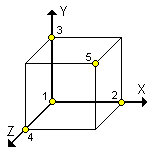
Теперь приступим к самому интересному. В прошлом шаге мы познакомились с сеткой точек, координаты которых жестко закреплены параметрами ячеек сетки. Узел IndexedFaceSet позволяет построить поверхность (а вернее практически трехмерное тело) по заданному набору точек. Узел описывается следующим образом:
IndexedFaceSet {
eventIn MFInt32 set_colorIndex
eventIn MFInt32 set_coordIndex
eventIn MFInt32 set_normalIndex
eventIn MFInt32 set_texCoordIndex
exposedField SFNode color NULL
exposedField SFNode coord NULL
exposedField SFNode normal NULL
exposedField SFNode texCoord NULL
field SFBool ccw TRUE
field MFInt32 colorIndex []
field SFBool colorPerVertex TRUE
field SFBool convex TRUE
field MFInt32 coordIndex []
field SFFloat creaseAngle 0
field MFInt32 normalIndex []
field SFBool normalPerVertex TRUE
field SFBool solid TRUE
field MFInt32 texCoordIndex []
}
Как Вы видите этот узел содержит много параметров, но для задания простейшего тела нужны не все. Мы с Вами познакомимся только с некоторыми из них, а остальные рассмотрим позже.
Чтобы все было более понятным давайте создадим реальное трехмерное тело. Но для простоты не будем увлекаться трехмерными "лицами", а создадим достаточно простое всем знакомое платоново тело - икосаэдр (он имеет 20 граней, 30 ребер, 12 вершин). Нам надо с вами задать координаты для 12 точек. Строиться икосаэдр не сложно. Сначала берется окружность и делится на 5 равных частей, при этом получаются точки разбиения, которые будут точками икосаэдра. Вот так выглядит эта поделенная окружность:
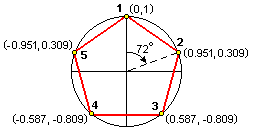
Для того. чтобы получить "объем" берется вторая окружность поделенная таким же образом, но только повернутая в противоположную сторону. Добавляются две вершины: сверху и снизу. Все эти точки соединяются ребрами. Получается следующая фигура:
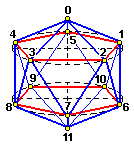
Плоскости, в которых лежат окружности расположены в плоскостях Y=-0.5 и Y=+0.5, при этом центр икосаэдра совпадает с центром координат. На рисунках специально указаны все координаты и пронумерованы вершины, для того, чтобы можно было не запутаться при создании массива точек.
Прежде чем создавать грани экосаэдра надо понять процесс задания этих граней. Грань (плоскость) в VRML задается перечислением как минимум трех точек лежащих на этой плоскости. Всем известно, что через три точки в пространстве можно провести только одну плоскость. Вы можете строить плоскости хоть из 10 вершин, но дело в том, что точность задания координат каждой вершины может привести к тому, что некоторые точки не будут лежать на задаваемой плоскости и иметь мельчайшие отклонения. Поэтому, чтобы не ломать голову расчетами уточненных координат плоскости лучше всегда задавать только тремя точками (вершинами). Те для кого линейная алгебра знакома, сразу же могут задать вопрос о нормали плоскости, а именно "куда направлена нормаль к плоскости" ? Правильный вопрос, ведь именно по нормали программа высчитывает освещенность плоскости, ее видимость для обозревателя и многие другие параметры. Чтобы указать направление нормали в VRML применяется порядок задания точек. Три точки определяющие плоскость задаются по правилу "буравчика". Давайте сначала посмотрим на рисунок:
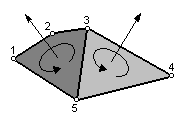
На рисунке изображены две плоскости и нормали к ним, направленные таким образом, чтобы эти плоскости были видимыми, т.е. нормальные вертора должны быть направлены в сторону наблюдателя. Еще вы видите направления вращения руки при вкручивании "буравчика". Теперь задание левой плоскости будет таким: 5 3 2 1, т.е. точки перечислены в порядке "вращения" вокруг нормали. Конечно же перечисление точек может начаться с любой точки, т.е. записи 3 2 1 5 и 1 5 3 2 задают одну и ту же плоскость, самое главное какая точка за какой идет по ходу вращения. Правая плоскость задается, как 3 5 4, и как видите для нее используется рекомендованное количество точек - три. В связи с тем, что количество точек может варьироваться от плоскости к плоскости разработчики VRML придумали признак-разделитель "-1", который следует после определения каждой плоскости. Например, определение двух этих плоскостей выглядело бы так: 3 2 1 5 -1 3 5 4.
Ну, а теперь давайте созадим массив точек икосаэдра и определим какие грани из каких точек состоят.
#VRML V2.0 utf8
WorldInfo {
info ["IndexedFaceSet example"]
title "Step 15 Example"
}
Background{
skyColor 0 0 0
}
Group {
children[
IndexedFaceSet {
# определяем набор из 12 вершин с помощь узла Coordinate
coord Coordinate {
point [
0 1 0 #0
.951 .5 -.309 #1
.587 .5 .809 #2
-.587 .5 .809 #3
-.951 .5 -.309 #4
0 .5 -1 #5
.951 -.5 .309 #6
0 -.5 1 #7
-.951 -.5 .309 #8
-.587 -.5 -.809 #9
.587 -.5 -.809 #10
0 -1 0 #11
]
}
#Определяем 20 граней икосаэдра
coordIndex [
0 2 1 -1 0 3 2 -1 0 4 3 -1 0 5 4 -1 0 1 5 -1
1 2 6 -1 2 7 6 -1 2 3 7 -1 3 8 7 -1 3 4 8 -1
4 9 8 -1 4 5 9 -1 5 10 9 -1 5 1 10 -1 1 6 10 -1
7 11 6 -1 7 8 11 -1 9 11 8 -1 9 10 11 -1 10 6 11 -1
]
}
]
}
Как Вы можете увидеть из примера, вершины перечисляются в параметре coord при помощи узла Coordinate. Грани же задаются в массиве coordIndex, где каждая грань отделяется от других -1. Получается такое вот тело:
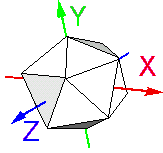
Я специально обвел ребра черными линиями, чтобы они были четко видны.
Некоторые поля узла IndexedFaceSet вам известны из предыдущих шагов. К таким полям можно отнести creaseAngle, solid.
С помощью creaseAngle Вы можете сделать тело сглаженным. Но если мы будем сглаживать икосаэдр, то просто получим из него нечто очень сильно похожее на обычную сферу, кстати можете посмотреть на нее в шаге 13 и увидите, что сфера в действительности просто сильно сглаженное платоново тело с большим количеством граней.
После возни с нормалями тела можно также понять смысл поля solid. В переводе это "целое" (твердое, прочное и т.д.), т.е. когда этот признак равен TRUE, то тело считается целиковым и значит в нем нет пустоты. По этому нормали всех граней тела должны быть направлены из его центра наружу. При этом считается, что грани имеют правильно направленные нормали, и если вдруг наблюдатель окажется внутри тела, то ни одной грани он не увидит, так как векторы нормали направлены от него. Если же вдруг поле solid будет равно FALSE и у тела не будет определена какая-то одна грань, то через эту "дырку" можно будет видеть все то, что творится с другой стороны, так как в таком случае грани будут считаться двух сторонними (иметь две нормали в обе стороны) и тело будет считаться пустым внутри.
Совместно с solid можно также и разобраться с полем convex, которое означает, что трехмерное тело выпуклое (TRUE). Это означает, что все грани плоские, не пересекают друг друга и внутренние углы между гранями тела меньше 180 градусов, иначе тело будет считаться вогнутым или очень сложным (позже я думаю посвятим этому отдельный шаг).
На этом пока все, остальные параметры мы с Вами рассмотрим чуть позже, когда вплотную займемся окраской и текстурированием. А пока вы можете тренироваться в создании сложных трехмерных тел.