Название ФАЛ является сокращением от "Функции Алгебры Логики". Что это такое с лету просто так не расскажешь :) Но я всеже попробую...
Пока давайте расскажу предысторию... Когда я писал "Шаг 7 - Сортировка Хоара", то старался получить такой вариант алгоритма, где по минимуму используется переменных, а соответственно операций присваивания тоже становится меньше. Но тут возникла небольшая проблемка... А именно сложность и громоздкость оператора сравнения if. Сами посмотрите внимательно, перестановка элементов происходит когда правый меньше левого. Но у нас то переменные всегда меняются местами и поэтому точно сказать на правый элемент или левый указывает base невозможно. Из-за этого пришлось делать сравнение двух переменных base и opposite. Из-за этого оператор сравнения разросся еще на одну скобку. Весь прикол оказался впереди, сложно все это объяснить, но если Вы внимательно подумаете, то окажется, что этих двух сравнений недостаточно и становится 4 скобки, вот таких:
if (
((array[base]<array[opposite])&&(base>opposite))||
((array[base]>array[opposite])&&(base<opposite))
){ ... обмен ...};
Т.е. как видите оператор сравнения вырос до неприемлимых величин. В нем аж 3 логических и 4 операций сравнения, т.е. всего 7. Понятное дело такая конструкция будет крайне не эффективна по быстродействию.
Вот когда наступило некое отчаяние я вдруг вспомнил интересную науку "схемотехнику", а ее единственная задача минимизировать функцию так, чтобы было меньше логических элементов. Так что решил применить зания в несколько другой "степи" :)
Прежде чем приступать к сложному надо сначала разобраться с основами. Всю математическую логику составляют 3 операции: отрицание - !, или - ||, и - &&. С помошью этих операций можно реализовать любую функцию алгебры логики, а если поглубже поизучать эту науку, то окажется что всего две. Значение возвращаемые этими логическими операциями Вы должны прекрасно знать, но для верности составлю таблицу истинности.
A B | !A | A || B | A && B -------------------------------------- 0 0 | 1 | 0 | 0 0 1 | 1 | 1 | 0 1 0 | 0 | 1 | 0 1 1 | 0 | 1 | 1
Теперь представьте, что каждая скобка со сравнением это отдельное событие A или B. Т.е. если при сравнении получается результат больше, то событие принимает значение 1 (единица), а если меньше, то 0 (нуль). Так вот всем нашим скобкам назначается определенная буква и составляется для всего оператора сравнения таблица истинности. Эта операция может быть достаточно сложной, потому что Вы должны правильно просчитать все варианты. Вобщем в результате получилась такая таблица истинности:
A = base > opposite B = array[base] > array[opposite] A B | рез. ---------------- 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0 ----------------
А потом поискав в голове методом пузырька :) эту конструкцию я был потрясен. Оказалось, что эта операция есть простое "исключающее или" и как в народе "деление по модулю 2". В результате всех этих умозаключений оператор сравнения уменьшился более чем в двое и стал занимать всего 2 операции сравнения и одну логическую (которая кстати для процессора все равно что И, ИЛИ или НЕ). Поэтому мы смогли получить большее быстродействие.
Ответьте на вопрос "могли лы вы просто смотря на значки больше, меньше и т.д. сказать что в результате получится XOR "? Наверняка скажете нет... Почти всегда голова от раздумий распухает настолько, что все начинают лепить трехэтажные формулы и выражения. Эта проблема считаю очень актуальна...
Вобщем в результате рассуждений пришли к самому методу... Метод называется "Карты КАРНО" :) Вся идея карты заключается в том, чтобы все возможные варианты расположить в одной табличке. На следующем рисунке показана нумерация таблиц Карно для 2, 3 и 4 переменных.
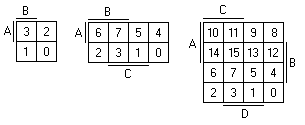
Нумерация таблицы такова, что например ячейке с номером 2 соответствует вариант, в котором A = 1 и B = 0. Заметили палочки над ячейками таблицы ? Они ограничивают такие зоны, в которых значение данной переменной всегда равно единице. Посмотрите...
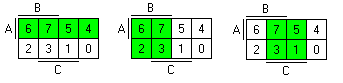
Видите какую зону охватывает переменная A(она зеленая) ? В двоичных записях чисел 6=110, 7=111, 5=101 и 4=100 первая двоичная цифра (а это и есть A) равна 1. Так вот вся таблица делится на зоны. На рисунке первая табличка для A, вторая для B, а третья для C...
Далее просто... Вы составляете таблицу истинности и заносите нулики и единички в клетки с номерами, десятичные значения которых равны двоичному значению набора переменных... Ё... Даже сам не понял %) Ну вобщем легче табличкой...
Ячейка | A B C ----------------- 0 | 0 0 0 1 | 0 0 1 2 | 0 1 0 3 | 0 1 1 4 | 1 0 0 5 | 1 0 1 6 | 1 1 0 7 | 1 1 1
Далее наступает еще более сложная операция - это нахождение контуров. Контуром тут называется область в табличке из единиц. При этом чем больше единиц попало в один контур, тем лучше. Количество единиц в одном контуре может быть только кратное двум, т.е. 1 2 4 8 ... Вот смотрите пример нахождения контуров...
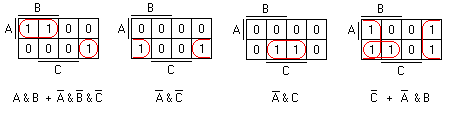
Тут очень много разных примеров... Существуют целые контуры, как на 1 рисунке и 3. А есть также разорванные как на 2 и на 4. Но разорванные они только с виду, а если мысленно склеить противоположные края таблицы, то контуры будут целыми %) Вобщем вся идея проста, но и одновременно сложна: Вам требуется обвести как можно больше единичек одновременно, и при этом сделать столько разных контуров, чтобы все единички были покрыты. Единички могут располагаться только в столбец, стороку или несколько столбцов и строк, т.е. "для одаренных" скажу иначе: "по диагонали контуры строить нельзя".
Теперь начинается самое прикольное... Это запись логического выражения. Давайте объясню на первом рисуночке.
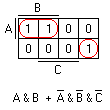
Вы видите контур вверху и контур на одну ячейку внизу справа. Давайте запишем формулу для верхнего контура. Для этого смотрим в какую область контур полностью попадает. В данном случае контур полностью попадает в область A и B, поэтому для него будет формула A & B. Нижний контур не попадает ни в одну из известных нам областей. Все такие области называются противоположными и получаются операцией НЕ. Например просто возьмите и проинвертируйте рисунок с областями, тогда у Вас темными(зелеными) окажутся противоположные зоны, а светлыми (белыми) прежние. Вобщем мы видим, что этот маленький контур попадает во все противоположные зоны, поэтому для него получится запись (!A) & (!B) & (!C). Весь же полученный результат записан на самом рисунке %)
Таким вот образом составляются эти карты Карно. Если Вы все хорошо сделали, то Вы получите самый наименьший результат из возможных. Тут также следует отметить, что контура можно рисовать многими способами и иногда приходится попотеть, чтобы найти верное их размещение. Понятное дело за 10 мин. этому не научиться... Нас же учили пол года !!! :)
Следуя этой методике и еще используя некоторые законы мат-логики можно получать Выражения значительно короче, чем первоначально. Столкнулся я с этим уже на этапе сортировки, а представьте, что делает программист создавая игру, в которой в зависимости от 3-4 условий (и их 23...24 комбинаций) персонаж может совершать много различных действий. Структуры CASE разростаются как невообразимое дерево, и программа увеличивается в сотни раз... А ведь может стоило просто подойти к этому с точки зрения математики ?! Подумайте над этим !!!