Тема нахождения пути на карте волнует многих программистов игр (в основном начинающих), но даже бывалые программеры делают свои алгоритмы не очень мобильными. Здесь я описал некоторые алгоритмы нахождения пути. Беря их за основу можно придумать много достаточно продвинутых алгоритмов. К сожалению идеального алгоритма не существует и поэтому ради использования того или другого требуется жертвовать либо производительностью либо тем достаточно небольшим интелектом который нужен для него.
Существует несколько методов нахождения пути на карте:
В играх довольно часто применяют маршрутный алгоритм (или его модификации) в силу его простой реализации и небольшого количества вычислений. Но он очень часто не страбатывает в сложной игровой ситуации и персонаж начинает дергаться из стороны в сторону тем самым раздражая игрока (по своему примеру в игре StarCraft). Применяя волновой алгоритм можно добиться большего результата, но волновой алгоритм для использования в играх требует небольшой доработки, ведь он не может строить трассу по диагонали. Можно совместить совершенство волнового и маневренность маршрутного, рассматривая 8-ми элементную окрестность вокруг фронта волны при построении трассы. Только вот вычислений здесь поменьше, ведь номер фронта волны уже и есть расстояние до начального элемента, значит можно просто выбрать наименьший элемент из окрестности и продвинуть трассу в его сторону. Но все же каким бы универсальным волновой алгоритм не был, единственный огромный недостаток на лицо - это необходимость большого количества памяти для хранения вспомогательной карты для фронтов волн и достаточно долгое построение пути для каждого персонажа. Для меньших затрат я лично использую уже просчитанную карту фронтов волн для всех персонажей, которые идут в одну точку, тем самым уменьшая время расчета трассы для каждого из них.
Волновой алгоритм (Алгоритм Ли)
Волновой алгоритм является одним из самых уникальных алгоритмов трассировки. Он позволяет построить трассу(путь) между двумя элементами в любом лабиринте.
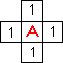 Рис 1. Рис 1. | Из начального элемента распространяется в 4-х направлениях волна (рис1.). Элемент в который пришла волна образует фронт волны.На рисунках цифрами обозначены номера фронтов волны. |
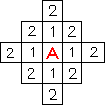 Рис2. Рис2. | Каждый элемент первого фронта волны является источником вторичной волны (рис 2.). Элементы второго фронта волны генерируют волну третьего фронта и т.д. Процесс продолжается до тех пор пока не будет достигнут конечный элемент. На втором этапе строится сама трасса. Её построение осуществляется в соответствии со следующими правилами:
|
Приоритеты направления движения выбираются на стадии разработки. В зависимости от того какими задаются эти приоритеты получаются разные трассы, НО длина трассы в любом случае остается одной и той же.
Преимущества волнового алгоритма в том, что с его помощью можно найти трассу в любом лабиринте и с любым количеством запретных элементов (стен). Единственным недостатком этого алгоритма является, то что при построении трассы требуется большой объем памяти.
Пример использования ВОЛНОВОГО АЛГОРИТМА:
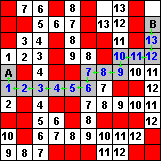
Красным цветом отмечены запрещенные элементы. Серым цветом трасса после действия алгоритма.
А-Начальная точка,В-Конечная.
Приоритеты движения ВЛЕВО,ВПРАВО,ВВЕРХ,ВНИЗ.
Построение трассы ведется от начальной точки к конечной. Приоритетные направления показаны зелеными стрелками.
Маршрутный алгоритм
Маршрутный алгоритм имеет две разновидности :
- Основанный на вычислении расстояния между точками.
- Основанный на рекурентном соотношении.
Маршрутный алгоритм получил свое название, потому что осухествляет одновременно и формирование фронта и прокладывание трассы.Источником волны на каждом шаге является конечный элемент участка трассы проложенной на предыдущих шагах.
Маршрутный алгоритм основанный на вычислении расстояния между точками.
Работа алгоритма начинается от начального элемента. При этом вокруг начального элемента рассматривается 8-ми элементная окрестность. От каждого элемента окрестности до конечного элемента оценивается длинна пути. При этом расстояние между точками вычислется по формуле:
D=|Xi-XB|+|Yi-YB|
где (Xi,Yi) - Координаты точки окрестности. (XВ,YВ)- Координаты конечного элемента.
Таким образом вычисляется восемь значений из которых выбирается минимальное. Элемент от которого расстояние оказалось минимальным выбирается в качестве элемента трассы. Вокруг него снова рассматривается 8-ми элементная окрестность. Процесс продолжается до тех пор пока не будет достигнут конечный элемент. Если на пути встречается препятствие в виде запрещенного элемента, то обход препятствия осуществляется исходя из интуиции разработчика. При этом задаются направления обхода препятствия.
Маршрутный алгоритм основанный на рекурентном соотношении.
Маршрутный алгоритм можно построить на основе следующего рекурентного соотношения:
y(x) = 2y(x + h) + y(x + 2h) + d
Где x,y(x) - абсцисса и ордината элемента занимаемого трассой на данном шаге.
(x + h) - ордината элемента занимаемого трассой на предыдущем шаге.
(x + 2h) - ордината элемента отстоящего от вычисляемого на 2 шага.
h - величина изменения абциссы на каждом шаге.
d (delta) - это функция определяющая вид трассы. Если d=0 то строится прямолинейная трасса, если d=const то строится параболическая трасса.
Ордината очередного элемента трассы вычисляется по рекурентной формуле, а абсцисса трассы вычисляется по формуле :
D=Xn=Xn-1+h
Знак "+" или "-" в рекурентной формуле выбирается исходя из того откуда начинается построение трассы, из начального элемента "+", и соответственно из конечного "-".
По этой формуле чтобы вычислить 3-й элемент трассы необходимо знать два предыдущих. Первым элементом является исходный элемент A(XA,YA), тогда ордината второго элемента вычисляется по формуле :
Y(X)=Y(XA)+ ((Y(XA)-Y(XB))/(XA-XB))*h
Если на пути встретится запрещенный элемент его обход осуществляется исходя из интуиции разработчика.
Главным достоинством маршрутного алгоритма является простота, а также возможность движения по диагонали.